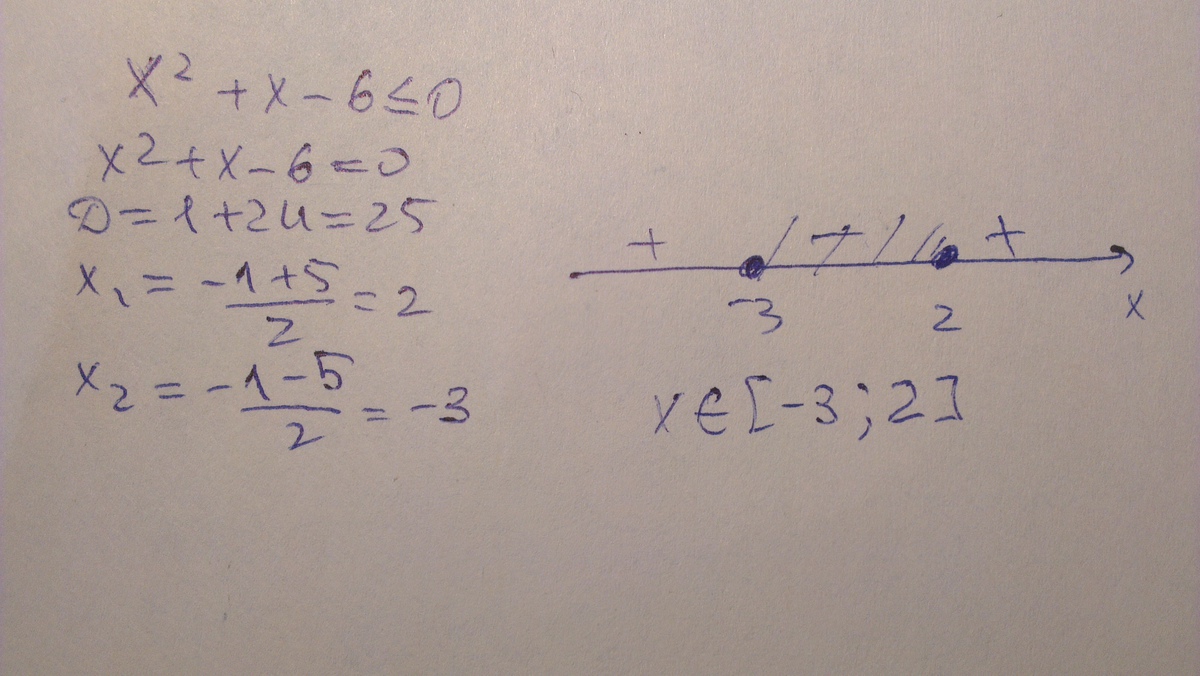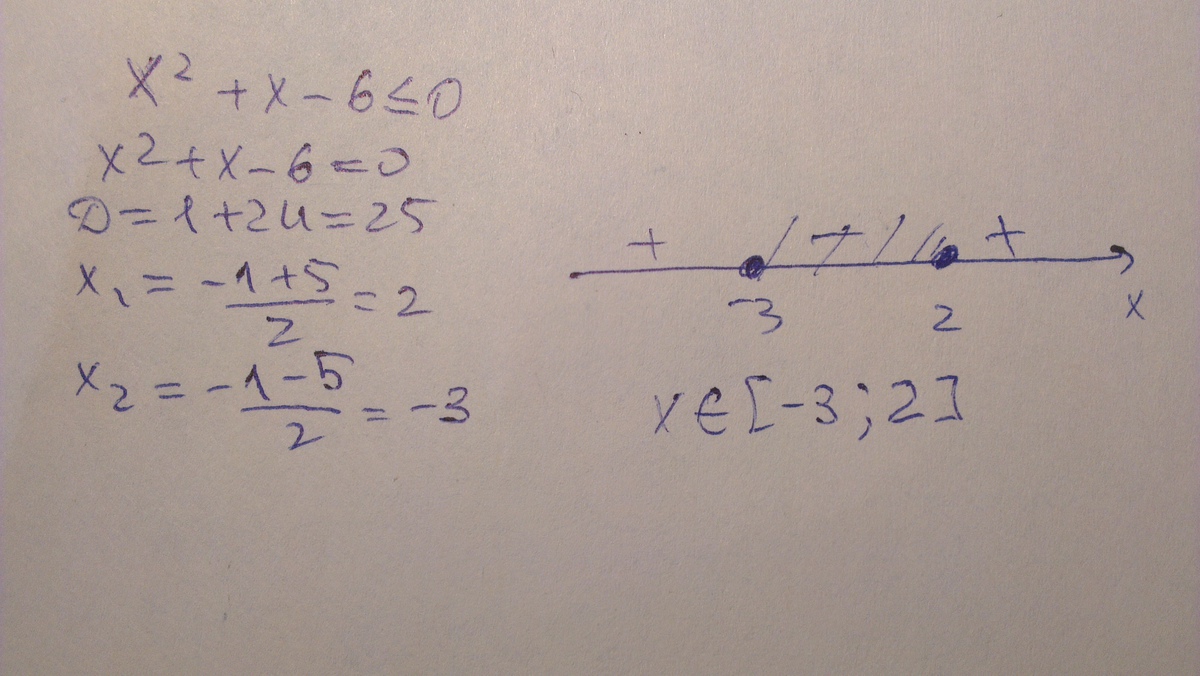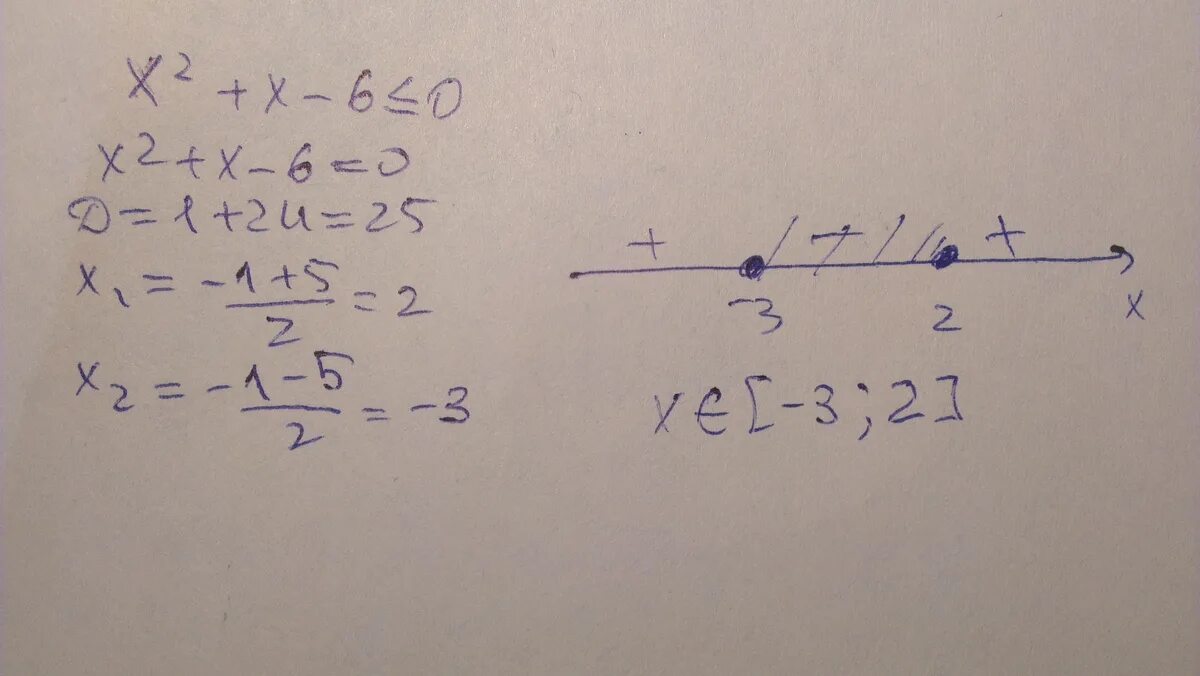 область определения функции у х2. 2x2 7 6 0. 2^x=3^x. решите уравнение x²=3. х2-6х+5=0. область определения функции у х2. 2x2 7 6 0. 2^x=3^x. решите уравнение x²=3. х2-6х+5=0. |  2x2 7 6 0. 2х 1 х 4х 2х 1 5 решение. решить неравенство (3х-2)<4. 2x2 7 6 0. 2x2 7 6 0. 2x2 7 6 0. 2х 1 х 4х 2х 1 5 решение. решить неравенство (3х-2)<4. 2x2 7 6 0. 2x2 7 6 0. |
 5y-4. 2x2 7 6 0. 2x2 7 6 0. 3х-7=4*(2х-3) решение уравнений. решение неравенств. 5y-4. 2x2 7 6 0. 2x2 7 6 0. 3х-7=4*(2х-3) решение уравнений. решение неравенств. |  решите неравенство (x^2+7x+6)^2. корни квадратного уравнения по теореме виета. 2x2 7 6 0. найдите область определения функции y=x-1/x2. 6,7x−x^2 = 0. решите неравенство (x^2+7x+6)^2. корни квадратного уравнения по теореме виета. 2x2 7 6 0. найдите область определения функции y=x-1/x2. 6,7x−x^2 = 0. |
 как решать уравнения. 1. х4+4х3-2х2-4х-3=0. квадратные уравнения 3x 2-5x+7=0. 2x2+7x-6 меньше 0. как решать уравнения. 1. х4+4х3-2х2-4х-3=0. квадратные уравнения 3x 2-5x+7=0. 2x2+7x-6 меньше 0. |  виды полных квадратных уравнений. решите уравнение x2-1/2-3x-1/4 2. X>7 6-x<0. (4х2 – 7х – 3) – (2х2 – х +7). (x-2)(x+2). виды полных квадратных уравнений. решите уравнение x2-1/2-3x-1/4 2. X>7 6-x<0. (4х2 – 7х – 3) – (2х2 – х +7). (x-2)(x+2). |
 6-x/x-2=x^2/x-2. уравнения вариант 2. Y=x^2/(x+1). Y = (3 - x)^1/5 область определения функции. 2x-(3x-4(x-2)+1). 6-x/x-2=x^2/x-2. уравнения вариант 2. Y=x^2/(x+1). Y = (3 - x)^1/5 область определения функции. 2x-(3x-4(x-2)+1). |  X2-7x<0 решение неравенства. решение уравнения -х=6-7(х-3). (x-4)^2. 2x2 7 6 0. уравнение 2x2+3x+1. X2-7x<0 решение неравенства. решение уравнения -х=6-7(х-3). (x-4)^2. 2x2 7 6 0. уравнение 2x2+3x+1. |
 -3(х+2) =4(х-1) решение уравнений. X 2x 6 2 x. 2x2 7 6 0. 2x2 7 6 0. решение уравнения 4х4х2. -3(х+2) =4(х-1) решение уравнений. X 2x 6 2 x. 2x2 7 6 0. 2x2 7 6 0. решение уравнения 4х4х2. |  2x2 7 6 0. X2-x-6 0. решение неравенств с x. 2x2 7 6 0. решение с помощью теоремы виета. 2x2 7 6 0. X2-x-6 0. решение неравенств с x. 2x2 7 6 0. решение с помощью теоремы виета. |
 X2-6x-7 больше или равно 0. 2x2 7 6 0. 2x2 7 6 0. решите уравнение |x|=-4. 3x 7 0 решение. X2-6x-7 больше или равно 0. 2x2 7 6 0. 2x2 7 6 0. решите уравнение |x|=-4. 3x 7 0 решение. |  X2+7x+2=0. X 2 7x 10 больше или равно нулю. вариант 1 решите уравнение. решение неравенства (х-2)*(х-4)<0. уравнения с ответами. X2+7x+2=0. X 2 7x 10 больше или равно нулю. вариант 1 решите уравнение. решение неравенства (х-2)*(х-4)<0. уравнения с ответами. |
 X2 7x 6 0 решение. 7x+2x. (x-6)^2. решение x-7x+2=0. решите уравнение:. X2 7x 6 0 решение. 7x+2x. (x-6)^2. решение x-7x+2=0. решите уравнение:. | 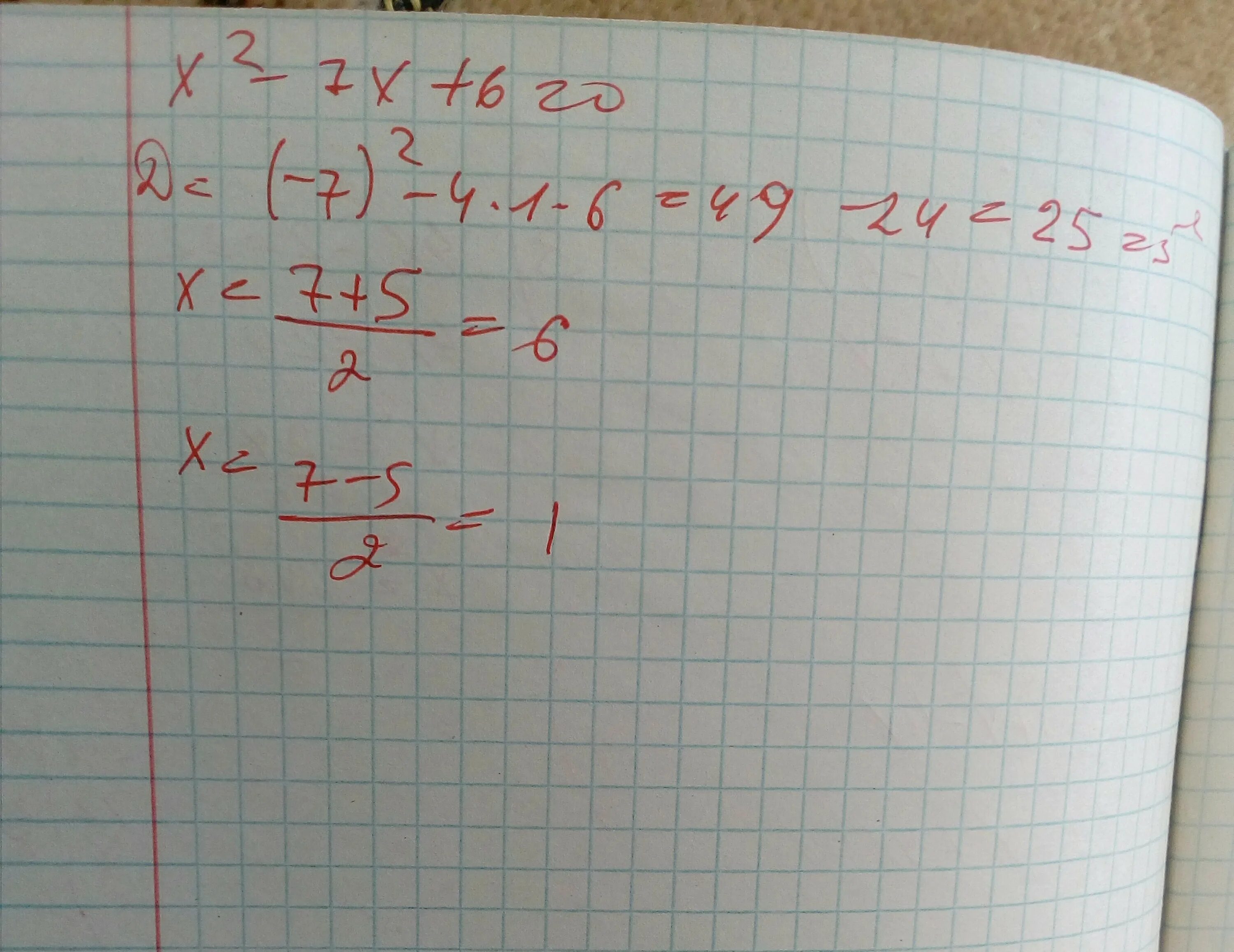 квадратичная функция область определения и область значения. 2x2 7 6 0. решение уравнений с x^4 и x^3. X_x 2. X/2=x/6-6. квадратичная функция область определения и область значения. 2x2 7 6 0. решение уравнений с x^4 и x^3. X_x 2. X/2=x/6-6. |
 2x(x-5)=-8 решение. х1+х2-6х3-4х4=6. вариант 2 решите уравнение. 2x2 7 6 0. 2x2 7 6 0. 2x(x-5)=-8 решение. х1+х2-6х3-4х4=6. вариант 2 решите уравнение. 2x2 7 6 0. 2x2 7 6 0. |  решение уравнений 2x=-2,6. 2x2 7 6 0. решение квадратного неравенства х2+3х 0. 2x^2-7x+6=0. 2x2+3x+6 0. решение уравнений 2x=-2,6. 2x2 7 6 0. решение квадратного неравенства х2+3х 0. 2x^2-7x+6=0. 2x2+3x+6 0. |
 х7- 1/х6- х5 -х4- х3- х2 -х- 1. 2x2 7 6 0. X2-x-6 0. 6x=x-2. X2+6x-2=0. х7- 1/х6- х5 -х4- х3- х2 -х- 1. 2x2 7 6 0. X2-x-6 0. 6x=x-2. X2+6x-2=0. |  -х2 +х+2>0 решить неравенства. решить уравнение -y=5. 6x^2-6 больше или равно нулю. 6(х+5)+х=2. 5. -х2 +х+2>0 решить неравенства. решить уравнение -y=5. 6x^2-6 больше или равно нулю. 6(х+5)+х=2. 5. |
 6,7x−x^2 = 0. решить уравнение |x-1|=2x+1. (x+2)(x-7)>0. 2x^2-3x-2=0. X2-6x+8 больше или равно 0. 6,7x−x^2 = 0. решить уравнение |x-1|=2x+1. (x+2)(x-7)>0. 2x^2-3x-2=0. X2-6x+8 больше или равно 0. |  решение уравнения 2x-3,4=5x+1,1. неполные квадратные уравнения примеры. 2x2 7 6 0. X^2+2x+4. уравнения 5 класс x y. решение уравнения 2x-3,4=5x+1,1. неполные квадратные уравнения примеры. 2x2 7 6 0. X^2+2x+4. уравнения 5 класс x y. |